1.1 Distances to Stars
When we look up into the night sky and see all the stars, many of which are suns similar to our own, they look fairly close together. But they’re not really close at all. The extent of space between them is huge.
Distance is an important and difficult quantity to measure in astronomy. We have to know how close we are to the stars and galaxies because much else in astronomy depends directly on that specific information — the total energy (luminosity) emitted, masses from orbital motions, stars’ true motions through space, and their true physical sizes.
Stars are so far away that even in telescopes they are only tiny points of light. Without a knowledge of the distance, you cannot accurately know whether you are looking at a small but very bright star or at a larger but less bright star, or whether this star or that is closer to us. This is also true of galaxies, quasars, jets and other distant phenomena.
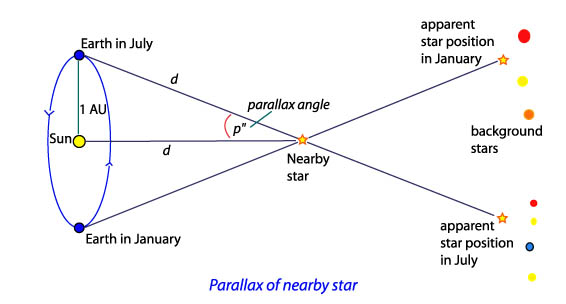
The distance between our eyes provides us our depth perception. Each eye must be held at a specific angle to center a subject. The brain interprets those angles and adjusts the eye’s focus, giving us a feel for how close the subject is and creating an in-depth image of the world around us. This biological angular detection is the basis of a distance calculation method called parallax in astronomy.
Triangulation, or trigonometric parallax, is a direct way of using the measured angular difference from two positions to measure the distance to some object. By observing a star’s position relative to the background stars from opposite sides of our orbit about the Sun, we have a wide baseline that will allow us to get an angular difference from observations 6 months apart and be able to measure the distance to something as far away as a star.
The Earth averages about 93 million miles from the Sun, so that is its nearly-circular orbit’s radius. This distance is often called an astronomical unit (AU) in astronomy. So the distance from one side of the Earth’s orbit to the opposite side is 2 AU, or about 186 million miles. When we measure the angle to the nearest star (Alpha Centauri) from one side of the orbit, wait six months, and measure it again, we find that the angular difference is rather small, requiring enormous precision of measurement. More on parallax and distance calculations here and here.
The European Space Agency (ESA) launched its automated Hipparcos satellite telescope to take measurements of over 118,000 stars during its lifetime from 1989–1993. Mission: improve the precision of catalogued locations of many stars and update the Tycho and Tycho 2 catalogs. Out of the newly measured parallaxes, 20,870 stars met the criterion of having a stellar parallax error of 10% or less.
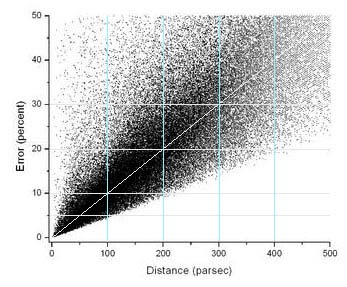
HIPPARCOS satellite parallax error plot by Ralph Biggins, from ESA/HIPPARCOS catalog data. Note increasing percent error bounds (vertically expanding wedge) with increasing distance
Even with the more accurate Hipparcos satellite data, distance measurements to stars out to around 200-220 light-years have up to 10% error, and they are increasingly less accurate out to about 500 light-years. Beyond that, trigonometric parallax measurements should not be considered reliable. Pogge, in the link above to his Lecture 5, claims Hipparcos data give “good distances out to 1000 light-years”, yet an estimated distance of only 500 light years with ±20%–30% error is already off by too much to be of much use. 1000 light-years is an almost incomprehensible distance, yet it is only about 1% of the way across our Milky Way galaxy.
An angle of one degree is subdivided into 60 minutes (60′) of arc, like the convention of dividing an hour into 60 minutes of time. Similarly each minute of arc can be subdivided into 60 seconds (60″) of arc. The parallax to all stars except our Sun is less than one arc second. In fact, the parallax to Alpha Centauri is about 0.75 of an arc second, or about 0.0002 degree. The parallax angle to all other stars is even less than this small value.
One light-year, the distance light travels in vacuum in one year, is almost 6 trillion miles. If you divide 3.26 by the parallax to a star in arc seconds, you will get the distance to the star as measured in light-years. Astronomers generally prefer parsecs (pc) rather than light-years as distance measurements, even though parallax measurements can only be used to determine distance accurately a relatively short distance from our Sun.
Example: (3.26 / 0.75 arc-second) = 4.36 light-years (ly), which is
25.65 trillion miles or 1.33 parsecs to the nearest star.
Let’s start closer to home.
1.2 Modeling Distances In and Near Our Solar System
Robert Burnham developed a model to show us in ordinary terms how much space there is out there between the stars. To understand its scale we need to know a couple of real distances.
As noted above, the distance from the Earth to the Sun is around 92,960,000 miles (149,605,000 km). Usually rounded off to 93 million miles (150 million km), this distance is called the Astronomical Unit (AU).
A light-year (ly) is equal to 63,294 AU. Coincidentally, this is about the same number as the number of inches in a statute mile, 63,360. Therefore, there is around the same number of inches in 1 AU (63,360 x 92,960,000) as the number of miles in 1 light-year (63,294 x 92,960,000). Those are really big numbers. Let’s stick to inches.
Burnham set the scale in his model so that 1 inch (1″) equals 1 AU or 93 million miles. Then 1 mile in our model would equal 1 ly. This scale would be expressed as 1:6,000,000,000,000. That’s one unit represents six million million units, which is a scale of one to 6 trillion or 1:6×10¹².
Let’s start describing a Burnhamesque miniature scale model of our solar system using this scale. We know the distance from Earth to the Sun (1 AU) will be one inch. How big will the Sun be? The Sun’s diameter is about 870,000 miles, so in our scale model the Sun will be a little under 1/100th of an inch across. That’s a very tiny speck. The Earth will be one inch away from the Sun but so small (0.00009″, or 9 one hundred thousandths of an inch) that we would not be able to see it without a microscope.
Pluto’s orbital radius is 39.5 times larger than Earth’s, so Pluto will be 39.5 inches, or almost exactly 1 meter, from the Sun.
The heliosphere, the region around the Sun which the solar wind permeates, is about 7 feet in our model.
So where is the nearest star in our model? Our nearest neighbor is Alpha Centauri, which is over 4 light-years away. That’s more than 4 miles in our model.
Yes, 4 miles. Our model Sun is one tiny speck, and it’s 4 miles to the next nearest speck. That’s a lot of space in between. So how big is our galaxy in this tiny model? The model galaxy would stretch 100,000 miles across. The thin disk and spiral arms would be a thousand miles thick. Its central bulge of stars would be well over 6000 miles from top to bottom. Our galaxy is but one of hundreds of billions of galaxies visible in the observable Universe with our present instruments. The nighttime sky appears to be crowded with stars, but stars are separated typically by over 10 million times their diameters.
1.3 Distance and Gravity
Remember that, as Newton wrote, the force of gravity decreases with (i.e., is inversely proportional to) the square of the distance between two objects. So the gravitational attraction between two specks 4 miles apart isn’t all that strong. Nor is the force of gravity between two stars 4 light-years apart. Let’s use Newton’s equation to work out what it actually is.
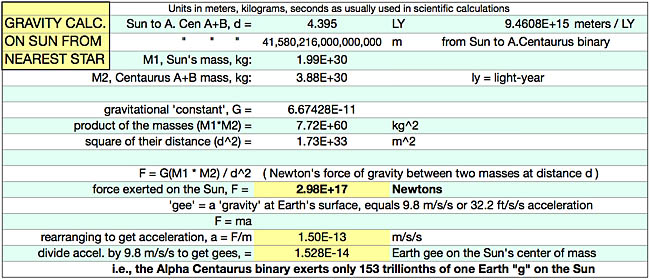
In the simple equation below, above the worksheet, F is the force in Newtons, G is a very small number called the Gravitational Constant, M1 and M2 are the estimated masses of the two stars in kilograms, and r is the distance between their centers in meters. Astronomers use the metric or S.I. system as it is much more widely used and more convenient than the traditional Imperial system of inches, feet, miles, pounds and ounces. However, the result of the calculation is presented at the bottom of the image in terms of the force of gravity at Earth’s surface, called a “gee” (for “gravity”) regardless of your measurement system.
F = G × (M1 × M2) ÷ r²
Despite their great mass, the two stars exert only a miniscule gravitational acceleration on each other. Whatever forces control the behavior of the matter in the universe must be strong enough and must be able to operate effectively enough over the immense distances involved.
Newton’s law of gravity has done well enough in explaining the forces of attraction and orbital motions within the limited area of the solar system. But the relatively weak force of gravity could only operate effectively, if at all, over interstellar distances if it were true that space is empty and there were no competing forces which might overcome that of gravity.
end of Chapter 1