Notes on the Holy Grail of Modern Physics

by Mathias Hüfner

While cleaning out my library, I came across the book “Three Roads to Quantum Gravity” by Lee Smolin from 2001. I read on the back cover:

The Holy Grail of modern physics is the theory of “quantum gravity.” It is the search for a view of the universe that unites two seemingly opposing pillars of modern science: Einstein’s general theory of relativity, which deals with large-scale phenomena such as planets, solar systems and galaxies, and quantum theory, which deals with the world of very small things – molecules, atoms and electrons…

I immediately remembered the scene from the Spielberg movie “Indiana Jones and the Last Crusade” where Indiana Jones had to choose the right goblet to bring his father the water of life. When I read Smolin’s book cover, I saw myself in the role of Indiana Jones for a moment, just like back then 20 years ago. I had to look for something very old among the shine of the lined-up drinking goblets. Only in Smolin’s book, it was not the choice of goblets, but three roads that he offered to choose from. In the book, the author described a road that did not lead to the goal, string theory. He took another road that he called loop gravity. He left me the simple, narrow, overgrown path that dispensed with the theory of relativity and quantum, analogous to the simple goblet, one of the goblets guarded by the last Templar Knight. The basic idea in Smolin’s book was to find, if possible, a universally valid equation for the movement of matter across all scales.

Today, 20 years later, I see that this path has led to fertile ground, namely the Electric Universe. But let’s look back. If Indiana Jones’ path of humility, trust, and the letter of the Lord led to the Grail, then on my path I had to observe criteria such as critical ability, attention to causality, and self-similarity as old research virtues in order not to succumb to the temptations of the glamour of fashion.

At the beginning of the 20th century, it became fashionable to announce spectacular things in physics and to try to prove them mathematically. The idea of separating mathematical truths from physical reality came about. Albert Einstein dreamed of surfing through the cosmos on a wave of light, and the quantum mechanics team around Werner Heisenberg wanted to describe this wave, and from this the theory of quantum gravity would emerge. But then insurmountable mathematical difficulties arose. – Why? Both physicists lacked a practical understanding of physical processes. They had skipped studying experimental physics and wanted to make up for this shortcoming by studying more mathematics. But this skipping had consequences for the history of physics, as I described in my book¹ (Götterdämmerung am Physiker-Himmel, Part 2.) The mathematical equations covered up the basic methodological problem. While Einstein, based on Newton’s point mechanics, only knew of linear motion, considered massless images and had to bend “space” to account for deviations from the straight line, quantum mechanics oriented itself on rotational motion. In rotations, a mass-effective moment of inertia must be taken into account. Thus, a unification of the two concepts is already ruled out.

When mathematics is applied to natural processes, mathematical results must also be plausible, since all mathematics is based on logic. Often, mathematical formulas describe something different from what their interpreters claim. For example, it is generally believed that Newton’s force law describes planetary motion, and because this is not the case, additional masses were invented in the last century. In reality, it only describes the one-dimensional force between two mass points without extension. It does not describe the rotation of a planet around the Sun or its own rotation. However, a planet is a physical body of spherical shape with a spatial extension. The movement of spheres can be observed in football games or table tennis competitions.

You can see that when you hit a ball, a spin is added to every trajectory, which makes the behavior of the ball when it hits the opponent’s side difficult to predict and thus increases the excitement of the game. Leonhard Euler first determined this spin in 1775. Both Newton’s and Euler’s concepts of motion belong together to the overall description of a movement when you consider the movement of a body in a potential field, because unlike in a solid vortex, where each part has the angular momentum of the entire system, in a potential vortex the total angular momentum breaks down into the sum of the individual angular momenta of its components. While Newton’s law of momentum is the product of mass and translational speed, Euler’s law of angular momentum is the product of moment of inertia and angular velocity. Newton’s force, which is the product of mass and acceleration, is opposed by Euler’s torque, which is the product of moment of inertia and angular acceleration. The kinetic energy of a ball is then composed of the translational energy and the rotational energy.

The second virtue is the acceptance of the law of causality and the asymmetries associated with it. Energy has its carrier in mass. Modern physics does not take this into account.

EQUATION #1

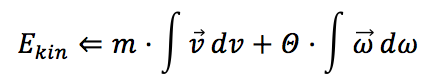
The reader may be surprised that I use the double arrow instead of the equal sign in (1). This is to bring the causal chain between force, momentum, and energy back into consciousness because at the beginning of the 20th century, it was believed that the world was symmetrical, as the first sentence of Einstein’s famous work on the Electrodynamics of Solid Bodies shows.

If we now think of the Eulerian spin of a tennis ball or the electron shell of an atom, then we have a hollow sphere with negligible thickness with radius r and mass m. Instead of the point mass, this has a moment of inertia . ² If the hollow sphere is moving with the velocity v rolling on the plane or flying through the air, its angular velocity is ω = v/r and consequently, its total kinetic energy is:

EQUATION #2

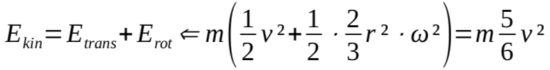
A number of scientists in the 19th century were involved in the development of the concept of energy, as it permeates the entire dynamics in all four phases of matter. In the 20th century two more terms came added: relativistic energy and radiation energy, expressed by Albert Einstein’s misunderstood formula and Max Planck’s formula with . Due to the moment of inertia, the factor is 0.7 for the solid sphere and 0.83 for the hollow sphere, where the total mass is in the surface. The actual total energy is smaller in both cases than that given by Einstein and Planck. It is not clear whether they meant the total energy, because Einstein always spoke of linear motion. For a deviation from the straight line, he had to use the “curvature tensor”. Planck’s energy formula clearly indicates rotational energy.

Max Planck is said to have been quite dissatisfied for several years with his equation E=h·ν defining the rotational energy of a quantum. As a serious scientist, he considered it important to understand the basis of the equation and its connection with classical mechanics and the Maxwell equations that he held in high esteem. This was perhaps the reason why he did not publish any scientific papers on black-body radiation for many years, nor the equation E=h·ν. When he finally did, nobody was able to establish the connection with classical mechanics, but Heisenberg claimed that the law of causality no longer applied in the microcosm. However, nobody wanted to find a limit where the scale transition from causal relationships to the realm of miracles lies.

On the contrary, these two energy formulas contributed more to the uncertainty of physicists than any other formula from the classical period, because they ignored the integration rules and initiated the transition to a discontinuous approach to physics. These uncertainties led to the first cracks in the physics community at the 1st Solvay Conference in Brussels in 1911, which was held under the motto Theory of Radiation and Quantum, which subsequently initiated the break with classical physics, with Antoon Lorentz’s force equation offering a good connection to Maxwell’s system of equations. (Fig. 1) Werner Heisenberg played a key role in promoting this break, as he described in his book Physics and Philosophy. ³

While Einstein’s theory of relativity was intended to symmetrize Maxwell’s equations and remove their dynamic character, Bohr and Heisenberg built a mathematical formalism that propagated the dualism of waves and particles that further disintegrated physics. Maxwell’s electrodynamics together with Lorentz’s force equation had already described the fundamental movements caused by electrical and magnetic forces.

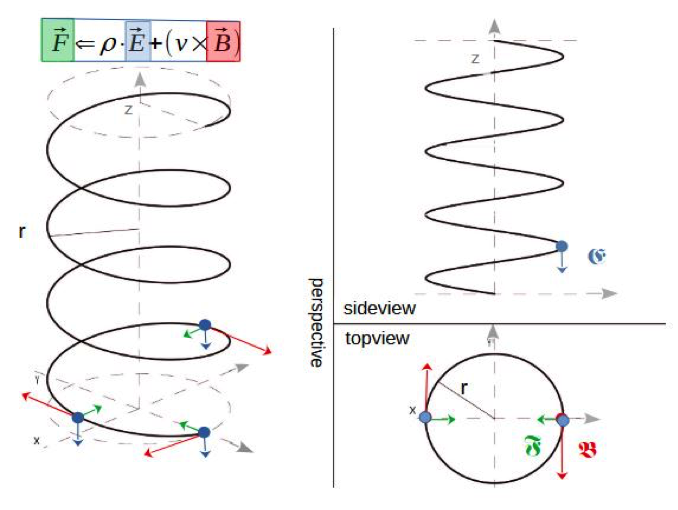
The third criterion is self-similarity. If Heinrich Hertz was able to experimentally confirm Maxwell’s equations in 1886 and their technical results are enjoyed today, is it not surprising that modern physics negates these equations at the atomic level just because Einstein disagreed in 1905 and found support from Lemaître and Planck? Were these gentlemen something like the Knights Templar in the Spielberg film, who were supposed to protect the Grail and lead the physics community astray? That would be a nice analogy but it is as untrue as the idea of quantum gravity is a holy grail.

So if the language and concept of a theory are not correct, no amount of mathematics can correct them

— D. E. Reinhardt ⁴

A fundamental question that arose from the equation for Planck’s black-body radiation was: Is a quantum of radiation an intrinsic property of the radiation or is it a property of the emission process? Today we know that it is a property of the emission process and that Planck’s constant h, the quantum of action, is not a natural constant. Not only the electron has a quantum of action, but every oscillating mass has its own quantum of action ⁵ (the proton as well as the hammer drill from the hardware store). Because atoms combine to form larger units due to their dipole character, they are also able to emit radiation themselves if they are stimulated to do so from outside. In 1886, Heinrich Hertz was the first to experimentally generate and demonstrate free electromagnetic waves, thereby confirming the correctness of Maxwell’s equations of 1864. However, this required an open oscillating circuit, which means that the ring current in the atomic shell had to be interrupted for a moment in order to generate an alternating current. For this to happen, neighboring atomic shells would have to collide with each other. In addition, for the transmission of the electrical impulse, an inductive coupling of all atomic shells in the surrounding area is required.

On the other hand, it is impossible to mechanically verify the radiation of an electromagnetic wave between two shells using Bohr’s atomic model. The ominous quantum leap was invented for this purpose. It should have been obvious that an atomic model with a constant quantum of action cannot explain a line spectrum if the orbital diameter of an atom increases due to excitation. This is because the moment of inertia of the rotating electron, which is included in the quantum of action, also changes. In return, the angular velocity must also change, but this does not then result in a discrete spectral line. On the other hand, the magnetic moment of the electron is constant and, according to Einstein and de Haas, identical to its moment of inertia except for a factor of 1⁄2.⁶

Then in 1924 de Brogli discovered the “matter wave”, after which the idea of the dualism of wave and particle was propagated by quantum mechanics. What he really discovered is the helical motion of a charge around the atomic nucleus. The electron charge flows like a vortex in a torus in a helical motion around the atomic nucleus, as illustrated in Figure 3, and as Helmholtz had already described in his vortex theory. Only a helical motion can be force-free. A wave motion requires a constant external supply of energy to maintain it. In order to emit an electromagnetic wave, the oscillating circuit must either be capacitively opened or there must be an inductive coupling between two magnetic coils. Capacitive transmission is not possible with atoms because the antenna dimensions are too large. The movement of the electron simulates a magnetic coil, so the inductive coupling to the neighboring atoms will probably play the decisive role in the transmission of light pulses. Why physicists who have their feet firmly on the ground want to describe this process from the electron’s perspective is a mystery to me. They call it a relativistic electron. They are at rest relative to the electron and should describe the process as they see it from their resting position. Physicists have mass, which is why they would never reach the speed of light. So why would they want to look at physics from an unrealistic perspective? I haven’t found a reasonable answer to that.

A black body can only emit wavelengths longer than 1mm if it has been supplied with energy of a shorter wavelength. Max Planck could certainly have made the connection to electrodynamics, because the necessary prerequisites had already been met in 1911, apart from de Broglie’s discovery. However, at the beginning of the 20th century, there was a lack of foresight. This foresight that only came about with the Internet and quantum mechanics was imposed on physics, an abstract mathematical concept that obscured the view of the physical facts.

According to Niels Bohr and Arnold Sommerfeld, Planck’s formula can also be written as follows:

EQUATION #3

This results in half an angular momentum, which is physically incomprehensible. If one were to take the integration rules into account , the world would be in order again and the quantum mechanical spin in addition to the magnetic moment would be superfluous, which it actually is, as measurements by Peter Galison⁷ have shown.

Galison writes:

In several careful experiments, Einstein and de Haas arrived at exactly the answer they expected, a result that is now considered to be almost half of what they should have found.

If we return to our basic idea of the motion of matter, then, taking into account the integration rule, we can note that an electron could move according to formula (2) as follows:

EQUATION #4

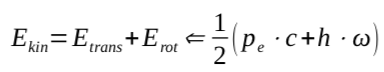
It remains unclear how large the respective energy share for translation and rotation actually is that is transmitted to the electron. The fact that we distinguish between different types of vortex suggests that the energy distribution between the two types of energy can change. Research into this is unknown. This formula also shows that there are two different concepts of motion between translation according to Einstein and rotation according to Planck, just as there are between Newton and Euler. The only difference is that the latter concepts of motion are practical and are combined in electrodynamics according to Maxwell and Lorentz, which has already permeated all areas of our lives. Equation #4 says nothing about the proton nor the interaction of the two particles. These few explanations alone go beyond the scope of understanding relativity and quantum mechanics, because the concept of translation and rotation of mass or charge must be thought of together across all scales and can only be realized in electrodynamics, where two forces are perpendicular to each other. Given the magnetic moment, the force-free motion is not straight but follows a closed, winding path, as any astronaut will confirm. Space does not have to be curved. In the quantum realm, an additional dimensionless spin number of 1/2 is superfluous.

Equation #4 demystifies the holy grail of physics. It turns out that the sacred mystery involves two widespread methodological errors that mathematics cannot correct. Mistakes and errors can always occur in the scientific process of discovery. It is bad, however, when mathematics, for ideological reasons, is used without a clear concept, and science loses the ability to self-criticize over generations where its representatives are stylized as untouchable idols.

---

Dr. Mathias Hüfner is a German translator volunteer for The Thunderbolts Project. He studied physics from 1964 until 1970 in Leipzig Germany, specializing in analytical measurement technology for radioactive isotopes. He then worked at Carl Zeiss Jena until 1978 on the development of laser microscope spectral analysis. There he was responsible for software development for the evaluation of the spectral data. Later he did his doctorate at the Friedrich Schiller University in the field of engineering and worked there 15 years as a scientific assistant. Some years after the change in East Germany, he worked as a freelance computer science teacher the last few years before his retirement.

Since 2015, Mathias has run a German website of The Thunderbolts Project http://mugglebibliothek.de/EU and his latest book is entitled Dynamic Structures in an Open Cosmos.

The ideas expressed in Thunderblogs do not necessarily express the views of T-Bolts Group Inc. or The Thunderbolts Project.

---

FOOTNOTES

1. M. Hüfner – Twilight of the Gods in the Physicist’s Heaven
   Publisher: Books on Demand, ISBN-13: 9783757817473
   ↩︎
2. https://de.wikipedia.org/wiki/Tr%C3%A4gheitsmoment
   (accessed on 16.06.2024)
   ↩︎
3. W. Heisenberg – Physics and Philosophy
   S. Hirzel Verlag Stuttgart 9th edition 2021 ISBN 978-3-7776-2153-1
   ↩︎
4. D. E. Reinhardt – Modern Physics and Philosophy of Science
   Summary of physics, metaphysics and mysticism; (accessed September 30, 2024)
   ↩︎
5. Unit: Js → kg m2/ s The unit of the quantum of action includes the mass. ↩︎
6. A. Einstein, W. J. de Haas – Experimental proof of Ampere molecular currents
   In: Proceedings of the German Physical Society. Volume 17, 1915, pp. 152-170 ↩︎
7. Peter L. Galison – Theoretical predisposition in experimental physics: Einstein and the gyromagnetic experiments 1915- 1925 – In: Historical Studies in the Physical Sciences. Volume 12, No. 2, 1982, pp. 285—323 (accessed on September 30, 2024) ↩︎