The Mystery of Gravity
by Mathias Hüfner
“People are not prisoners of their fate, they are prisoners of their thoughts,” Franklin Roosevelt once said. In today’s world, where everything is increasingly leading to specialization, we no longer understand the connections in nature because we can no longer overcome the narrow limits of our thought processes that we have followed a thousand times. We do not perceive mechanics, thermodynamics, and electrodynamics as the dynamics of nature, but as three different scientific disciplines that seem to have nothing to do with each other because different languages are now spoken in these disciplines. Gravity is still a mystery, from black holes to dark matter, because outside the planetary realm the law of gravity with velocity potential of the track speed does not apply without these auxiliary constructs. But why?
To gain clarity about the dynamics of the cosmos, we must delve into the history of physics. After Copernicus’ “De revolutionibus orbium coelestium” was first time printed in Nuremberg in 1543, replacing the old geocentric worldview with a heliocentric one, intensive observation of the sky began once the new hypothesis became known. One of the most important observers was the Dane Tycho Brahe. His collaboration with the young Johannes Kepler was of great importance for astronomy, as Kepler discovered his three laws of motion between 1609 and 1619 based on his very precise observations of the orbit of Mars. The observations were now supported by the invention of the telescope using a combination of lenses. Kepler combined two convex lenses. In 1609, Galileo used a replica of a Dutch telescope consisting of a convex and a diverging lens, which he aimed at Jupiter and studied the movement of Jupiter’s moons.
When Isaac Newton was able to explain in his Philosophiae Naturalis Principia Mathematica in 1687 that the apple falls to earth as a result of gravitational attraction, he was still using Kepler’s constant in his force law. He did not yet know why the moon stays in the sky and always faces us with the same side. He explained it with the inertia of everybody, based on the interaction of active, immaterial divine “natural forces” with absolutely passive matter – which became the basis of the scientific worldview of many generations. It was not until around 230 years later that Albert Einstein dispelled Newton’s idea of absoluteness by introducing variable reference systems, but retaining the immaterial character of the natural forces and reinterpreting the medieval spheres as a curvature of space.
Developments on the European mainland were different. In 1775, Leonhard Euler introduced the law of angular momentum as a fundamental principle in mechanics independent of Newton’s laws. In 1784/85, Charles Augustin de Coulomb used this to find a method of measuring the force between of two electrically charged masses using a torsion balance. He based his work on Newton’s law of force. The torsion balance was already used as a foliot1 in medieval clocks. Coulomb’s important preliminary achievement was determining the torsional tension of the wire used, which he reports on in his first memoir.2 Leonard Euler, today known only as a mathematician, also made discoveries in fluid mechanics in the mid-18th century. We owe him point mechanics and the introduction of angular momentum into mechanics. Now vortices could also be described. In addition to potential vortices, he also pointed out solid vortices, especially in connection with electrical currents in these fluids.3 as Hermann von Helmholtz noted in his vortex theory a century later. Euler was also the one who contradicted Newton’s corpuscular theory of light and inspired Christiaan Huygens with his wave theory of light.4
In 1798, Henry Cavendish succeeded in determining the gravitational constant using a torsion balance specially constructed by John Michell for the much weaker gravitational forces. The ratio of forces between electrical and gravitational forces is 1 to 1036. Based on the same measuring principle for mechanical and electrical forces, attempts were made to explain the developing electrodynamics mechanically. Newton’s influence on the thinking of physicists was too strong. Wilhelm Weber added an acceleration term to Newton’s force law, but the law remained one-dimensional.
In 1893, Oliver Heaviside introduced vector notation into mathematical physics. This gave forces directions.
“Matter is characterized by the property of inertia, which leads to it tending to remain in the state of motion that it possesses; and any change in the direction of motion is due to the action of a force, the actual measure of which is, therefore, the rate of change of the kinetic quantity or momentum“ 5
Oliver Heaviside
Heaviside also introduced the vector operators div for divergence and curl for rotation, which made Maxwell’s system of equations much clearer. This made it possible to represent entire vector fields. The divergence operator describes a source flow and the rotation operator a vortex.
Matter is mass in motion. Matter has three forms of motion, force, momentum, and energy, which is realized by the mass as a carrier. But mass is not a thing, but a basic relation. The question must be asked: mass of what? Since the mass of atoms is uncountable, a reference unit is needed. Since 1878, a platinum cylinder has been used for this purpose, symbolizing the mass of one kilogram. All masses are then compared with this standard unit. Countable quantities of atoms, or more precisely of charge carriers, are called quanta. A quantum is a countable quantity. Charges are usually bipolar and attractive or repulsive forces occur between the charge carriers. Neutrality means a charged equilibrium. A single free atom should have a charged equilibrium and thus react neutrally to its environment. An electron orbits a proton. But the moment two hydrogen atoms meet, the charges become unbalanced and two dipoles are created that attract each other. Neutral atoms always become dipoles that attract each other because the charges of the nucleus and shell shift but are bound by the magnetic moment. The resulting outward force is the mass-attracting gravitational force.
Cavendish’s spheres had no free electrical surface charges. Nevertheless, they attract each other with a very weak force. Coulomb had a completely different experience. He rubbed the spheres to remove electrons from the surfaces. Depending on the charge distribution of both balls, the forces generated are strongly attractive or repulsive. Gravity alone is therefore a residual electrical force that guarantees the cohesion of atoms due to their dipole effect between nucleus and shell, as the Italian physicist Ottaviano Fabrizio Mossotti already suspected in his 1836 work Sur les forces qui régissent la constitution intérieure del corps.6 If there were no free electrical charge in the plasma state of matter, the world might have collapsed. Behind the mass of atoms, there is always their charge, which is responsible for the forces. We now have the historically necessary physical elements together to solve the problem of gravity. Gravity is a source of force that occurs in connection with rotation. According to Newton’s equation, the moon would have fallen from the sky like the apple because he treated the force as a one-dimensional case. There is no mention of rotation in his formula. He still trusted in immaterial inertia and not in the conservation of angular momentum.
In a rotating system, we distinguish between the orbital angular momentum and the intrinsic angular momentum of the moving body. The angular momentum always refers to the point in space that is chosen as the reference point for the rotational movement. In a freely rotating system, the center of gravity is chosen as the reference point. In astronomy, this is usually the center of gravity of the central star or a galaxy. Due to the principle of inertia, every momentum is a conserved quantity and a force is required to change it.
If a plate rotates and a test body is on it, the angular velocity is constant over the radius. The orbital velocity is then the product of the angular velocity and the radius. This means that the orbital velocity increases with the distance from the center. But what about the rotation of the test body? It does not rotate on the plate. It always shows the same side to the center of rotation as the moon shows the Earth. We call such a vortex a rigid-body vortex. The centrifugal forces can be neglected. As Euler already determined, electromagnetic forces between the rotating bodies and the force center are necessary.
The complete opposite is the irrotational vortex, whose angular velocity and orbital velocity decrease with distance from the center. The centrifugal force reaches or exceeds the strength of the gravitational force. A body in this system acquires its angular momentum since the side of the test body facing away from the center of rotation rotates more slowly than the side facing the center of rotation.
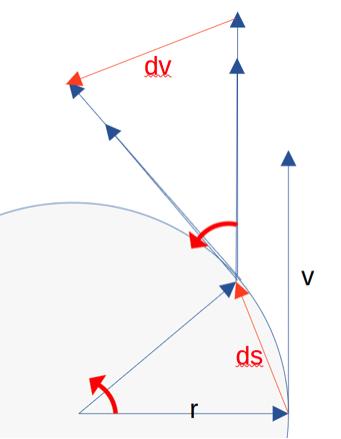
Determination of centrifugal force. As can be seen from Figure 1, according to the similarity theorem of geometry, dv/v = ds/r. If you multiply this equation by v, you get dv = ds∙v/r. The rotation takes place in time dt without the magnitude of the speed changing
dv/dt = ds/dt v/r
A radial acceleration with the value v²/r acts on the test mass. However, ds is an approximation for the radian measure rad. Consequently, ds/dt represents the angular velocity ω, which results in a conserved quantity together with the mass.
To achieve force-free rotation, two things must be fulfilled.
• The amounts of centripetal and centrifugal force must be in balance.
• The angular momentum must be conserved.
The latter condition was already known to Leonard Euler, but has obviously been forgotten in school physics! Engineers who put satellites into orbit, however, have remembered it.
For a test mass mp, therefore, |Fp | = |Ff | must hold, then according to Newton, Fp and according to Euler, Ff.
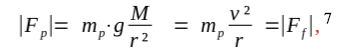
where v²/r is the escape acceleration g’ and v is the orbital velocity of the test mass. It should be obvious that according to Newton’s second force law, the expression gM/r² represents the centripetal acceleration.
Using v, you can now get the orbital velocity from the two formulas above necessary to overcome the attraction and let the test mass orbit the center of force.
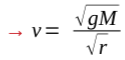
If we multiply this equation by √r, we get a constant velocity that keeps a test mass on a force-free path.
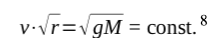
This contradicts the long-held idea of a universal gravitational constant in the cosmos
since there are many gravitational centers around which other bodies rotate.
We want to check whether the above equation is plausible.
The planets move (approximately) in a circular orbit around the Sun. This circular movement is weightless or force-free because the centripetal and centrifugal forces are in balance. If you look more closely, the planetary orbits are not circular orbits but elliptical orbits. The elliptical orbits are caused by the Sun moving in a galactic plasma stream, almost perpendicular to the eclipse. This causes the planets to move at different speeds depending on their position relative to the sun. The values given in the table are therefore the average speeds on a helical orbit in interstellar space.
To determine the vortex character of the planetary system, we need to know the average distance of the planets from the sun and their average orbital speed. We can find this data in the tables for the planet descriptions on Wikipedia9. To avoid manipulating unnecessarily large numbers, I give the radii in distances from the Earth to the sun, the astronomical units. (1AU ≈ 150˟106 km) From this, the angular velocities for the individual vortex models can be calculated. Remarkable that the earth-like planets have little to no rotation, whereas the large planets have a strong rotation. This is shown in the following table:
If the planets were rotating according to the laws of a irrotational vortex, the Sun would have to have the greatest angular velocity. This is not the case. Otherwise, the angular velocity does decrease. But the properties of a rigid-body vortex are not recognizable either. Although the planets Mercury and Venus hardly rotate about the Sun, their angular velocities differ considerably. There is no sign of the conservation of angular momentum, which suggests that there are previously unconsidered forces within the planetary system. The Pioneer probes also provide evidence of this, showing deviations from the predicted orbit. A slight acceleration towards the Sun was found.10 We find a constant for this if we multiply the orbital velocity by the square root of the distance from the Sun. It is a Kepler vortex.
We remember: Behind the mass of atoms there is always their charge, which is responsible for the forces. There is the residual charge of the volume and the surface charge of the free electrons.
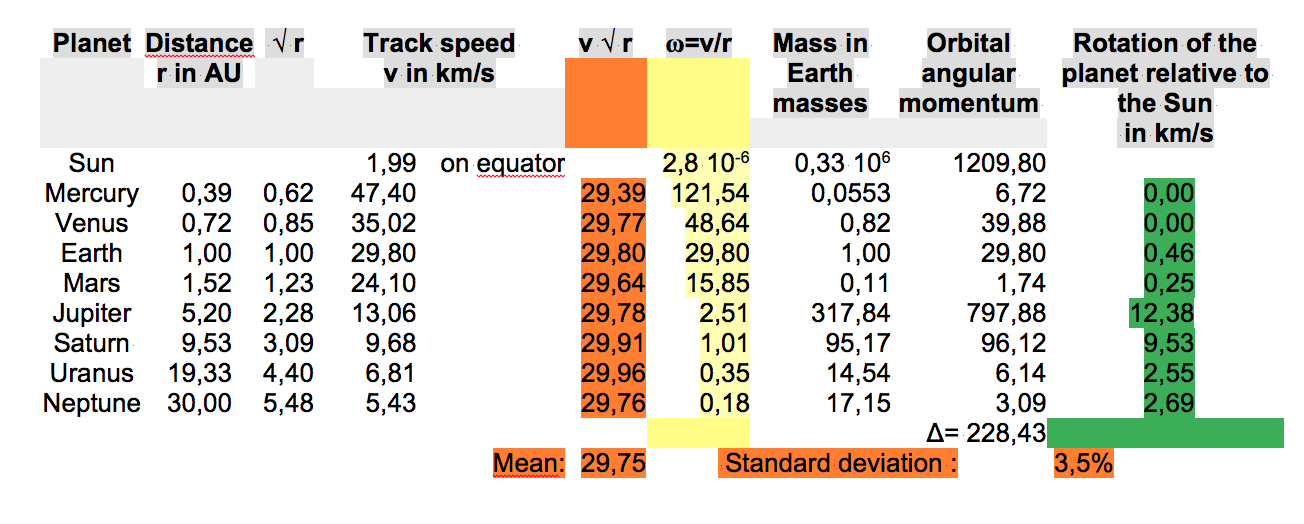
We now assume that the conditions in our planetary system can also be transferred to larger structures. By replacing the mass in the above formula with the product of the volume and the mass density of the sphere, we get:
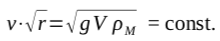
What happens now if the volume of the central sphere breaks down into smaller and smaller spheres? Then the volume remains constant, but the surface area grows. Let us substitute for the volume V the formula for the sphere and then for 4π r² the surface area OK.
Considering that the cosmos is an electric plasma with central positive charges and negative surroundings, we call the ratio of ρQ/ρM the degree of ionization J of the plasma. We set g → 1/4π∙ε0, for ρM, we set ρQ /J and, obtaining as the upper limit of the velocity:

The track speed is proportional to the square root of the surface area of the stars involved in the vortex. This is shown by the red curve in Figure 2.
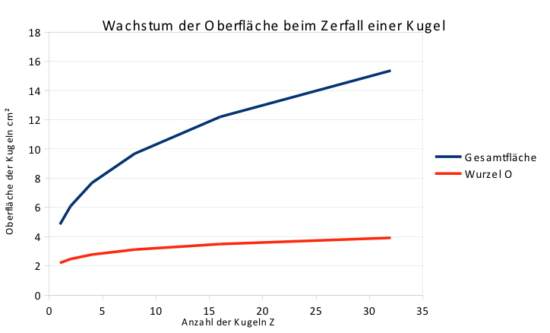
Figure 2: Growth of the surface with division of the mass into smaller spheres
The stellar density ρM depends on the structure of the galaxy and decreases towards the edge. Unlike in Newtonian mechanics, the value g depends on the surface charge of the stellar mass. This results in different velocity profiles, as shown in Figure 3.
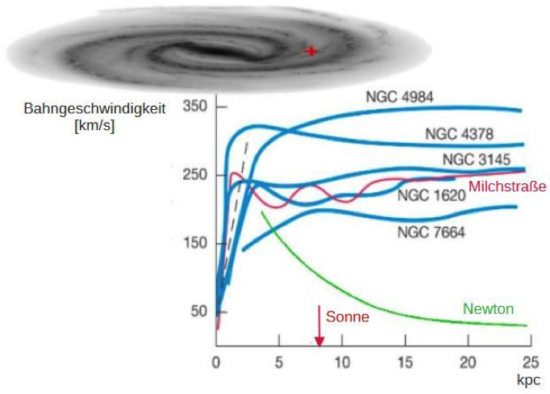
The undulations of the velocity profiles, particularly pronounced in the Milky Way, indicate that the galaxy arms rotate around their vortex filaments. This phenomenon, observed as the migration of the North Star, is incorrectly called precession11. If the balance between centripetal and centrifugal force is disturbed only slightly in favor of the gravitational force, the orbital speed is slowed down. If one concludes from this that a black hole would be created, this is only the result of two-dimensional thinking. The velocity vector has three components in space. If we take a cylindrical coordinate system, we get for the speed![]() If the components vr and vω become smaller, the result is that the component vz in the center must become very large due to inertia, as can be seen in Figure 4. It shows the galaxy M87 with a jet stream from its center.
If the components vr and vω become smaller, the result is that the component vz in the center must become very large due to inertia, as can be seen in Figure 4. It shows the galaxy M87 with a jet stream from its center.

While Newton’s mechanics requires more and more mass to explain celestial mechanics, knowledge of the electric surface charge is enough to explain the actual forces at work. While Newton’s and Euler’s mechanics still represent two different concepts, they are combined at the level of electrodynamics to form the Lorentz force. It is also the force that can describe all vortex movements in fast-flowing fluids, because the mass of the atoms is always behind their charges. But modern physics, with its approach to the Christian faith at the beginning of the 20th century, took a different path that brought more problems than solutions to understanding.
NOTES
1 The foliot is a regulator that provided an almost uniform rate in the earliest wheel clocks from around 1300
2 A.K.T. Assis – Coulomb’s Memoirs on Torsion,’Electricity, and Magnetism; https://www.ifi.unicamp.br/~assis/Coulomb-in-English.pdf
3 H.v. Helmholtz – Über Wirbelbewegungen; In Oswalds Klassiker der exakten Wissenschaften Bd.1 Reprint Bd.79 1858 Harry Deutsch Verlag
4 D. Speiser – Eulers Schriften zur Optik, zur Elektrizitat und zum Magnetismus; https://link.springer.com/chapter/10.1007/978-3-0348-9350-3_10
5 O. Heaviside – A GRAVITATIONAL AND ELECTROMAGNETIC ANALOGY; http://swissenschaft.ch/tesla/content/T_Library/L_Theory/Gravity/Gravitational%20and%20Electromagnetic%20Analogy.pdf
6 O. F. Mossotti – Sur les forces qui régissent la constitution intérieure del corps; https://search.worldcat.org/de/title/sur-les-forces-qui-regissent-la-constitution-interieure-des-corps/oclc/562587169
7 Derivation of centrifugal acceleration https://studyflix.de/ingenieurwissenschaften/zentripetalkraft-und-zentrifugalkraft-1526
8 Kepler constant – according to Johannes Kepler’s third law of 1609
9 https://de.wikipedia.org/wiki/Liste_der_Planeten_des_Sonnensystems
10 https://en.wikipedia.org/wiki/Pioneer_anomaly
11 Precession is the conical path of an axis of rotation when a deflecting force acts at one end of the axis of rotation and another force holds it in place at the other end.

Dr. Mathias Hüfner is a German translator volunteer for The Thunderbolts Project. He studied physics from 1964 until 1970 in Leipzig Germany, specializing in analytical measurement technology for radioactive isotopes. He then worked at Carl Zeiss Jena until 1978 on the development of laser microscope spectral analysis. There he was responsible for software development for the evaluation of the spectral data. Later he did his doctorate at the Friedrich Schiller University in the field of engineering and worked there 15 years as a scientific assistant. Some years after the change in East Germany, he worked as a freelance computer science teacher the last few years before his retirement.

Since 2015, Mathias has run a German website of The Thunderbolts Project http://mugglebibliothek.de/EU and his latest book is entitled Dynamic Structures in an Open Cosmos
The ideas expressed in Thunderblogs do not necessarily express the views of T-Bolts Group Inc. or The Thunderbolts Project.












