|
|
Since plasma is a superconductor, doesnít that mean charges
instantly neutralize and electric fields canít exist inside it?
|
|
|
Short Answer
No. Superconductors are materials that do not hinder the flow of
electric current. They have precisely zero resistance (the measure
of a material's opposition to the flow of electric current) and the
current will continue to flow almost indefinitely with no additional
energy input required. Electric currents that flow through plasma
experience non-zero resistance and will eventually cease if additional
energy is not added, therefore plasma is not a superconductor.
Owing largely to the fact that plasma is not a superconductor,
regions with non-neutral charges do not "instantly neutralize."
It is known from experimental plasma physics in the laboratory that
electric fields do exist between discrete localized regions of differing
charge inside an overall "quasi-neutral" plasma.
Long Answer:
For years it was assumed that plasmas were perfect conductors and now
astronomers and astrophysicists have come to treat plasma as though it
is a perfect conductor (superconductor) and any charge imbalance will
be "instantly neutralized." Sadly, for such an 'elegant' theory,
the only true superconductors that have been created in the lab have been
achieved using cryogenic temperatures (approaching 'absolute zero'). The
more we can reduce random (thermal, collisional) motion, the better the
conductivity will be. However, plasmas contain high 'temperature' electrons
and ions. Unfortunately, the thermal motions of charge carriers in a current
will still cause them to occasionally crash into one another.
The electrical conductivity of any material, including plasma, is
determined by two factors: the density of the population of available
charge carriers (the ions) in the material, and the mobility of these
carriers. In any plasma, the mobility of the ions is extremely high,
meaning that the charge carriers (the +ions and -electrons) are
extremely free to move. This gives plasma a high conductivity.
The trick with plasma is that it tends to be very low-density,
therefore conductivity is less than 'ideal' in plasma. Despite
being a very good conductor, plasma is not a perfect conductor
(it is not a zero-resistance superconductor).
This can be demonstrated simply by applying the mathematical
definition of resistance to the diagram of plasma discharge modes.
Resistance is defined by the equation R = V / I. Resistance R
(measured in ohms) is the ratio of voltage V (measured in volts)
to current I (measured in amperes).
|
|
|
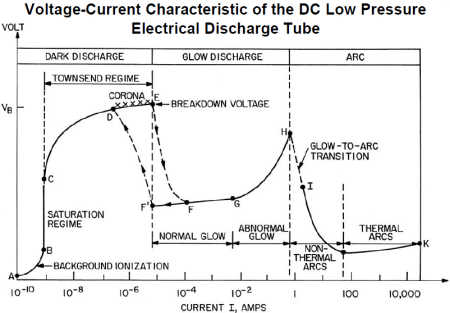
Plasma discharge regimes.
[Click to enlarge]
|
|
|
It is quite clear from the diagram above that if you draw a line from
the origin of the graph in the lower left to any point on the diagram
of plasma's discharge regimes, the slope of the line (V / I) will always
be positive and non-zero. That is to say, the diagram never touches the
X axis at any point. Voltage V never decreases to zero. Ergo resistance
R never decreases to zero. Ergo plasma is not a superconductor.
We now know that there can be slight voltage differences between different
points within plasmas. Non-trivial electric fields can and do exist inside
plasmas.
Many astrophysicists are still unaware of this property of plasmas, and
so, we often still find many incorrect assumptions and assertions in
astrophysical papers and popular news stories. If astrophysicists would
do away with the inapplicable notion that plasma is a superconductor and
acknowledge that electric fields can exist within plasmas, perhaps they
would then also realize that (as a corollary) magnetic fields cannot be
"frozen in" to plasmas but must be dynamically generated by
electric currents therein.
These more accurate understandings may open an entirely new vista for
researches into the astrophysical machinations of the cosmos at large,
of which up to 99.999% of the observable constituents are known to be
in the plasma state.
|
|
|
Permalink to this page
Return to index
|
|
|
|
|
|
|