Perceiving Einstein
Apr 27, 2010

We all know that Albert Einstein invented Special Relativity (SR) and its extension, General Relativity (GR). But what are they? Are these theories correct? Are they useful? Does it take a physicist or mathematician to understand them? Typically, any search of your local library or the Internet for a clear explanation of what Relativity Theory is all about usually falls quickly into a tangle of concepts such as Minkowsky space, time dilation, and other hypotheses – all impenetrable for the uninitiated. Or at least they have been up to now.

For years I have sought a simple explanation of these ideas. That search has been discouragingly unproductive. Early on I became aware that both SR and GR are controversial. Opinions on both sides of the question of their validity are intense. On one side, cosmologists and astrophysicists accept, defend, and use Einstein’s ideas to further their own work. They claim absolute success for models that result from their use of his theories. They disparage anyone who deigns to question the soundness of their beliefs.

Several non-believers^{1, 2} claim to have identified chinks in the body armor of Einstein’s work and in the validity and precision of later experiments that allegedly support it. But, understanding the thrusts and counter-thrusts of these arguments requires proficiency in graduate-level math through tensor analysis. Therefore, until recently, even the well-educated, interested reader has been unable to really understand this and thus has had no chance to develop an informed opinion. This all changed for me when I read a book written by astronomer Hilton Ratcliffe.

In the eleventh chapter of his first book³ Ratcliffe presents an account of some of the fundamental issues, assumptions, and goals that prompted Einstein’s work. He does this using only words – without mathematics⁴. For me these pages provided an opening key to the arcane concepts that had eluded me for so long. Ratcliffe starts by pointing out that one of Einstein’s primary assumptions or goals (it is not clear which) was to show the impossibility of the existence of absolute universal time and the real simultaneity of events.

One of the necessary tools for evaluating Einstein’s argument is the concept of the “reference frame” and what happens when two such frames move relatively to each other.

Take three one-meter rulers. Arrange two of them, lying on your desk, at right angles to each other. Now set the third ruler vertically at the junction of the first two and secure them all to each other so the (90°) angles between them are fixed. Name the two horizontal rulers x and y. Call the vertical ruler z. The instantaneous position of any object (a fly, a dust mote, etc.) can be uniquely defined by measuring its distance out along each of the rulers e.g., x = 3 cm, y = 4 cm, and z = 8 cm. This defines the position of the object. The set of rulers thus provides a “frame of reference” in which the location of any point can be described. Any change in this position measures the “motion” of the object in this frame of reference. Of course the rulers must be straight and the gradation marks along them must be equally spaced and not move with respect to one another.

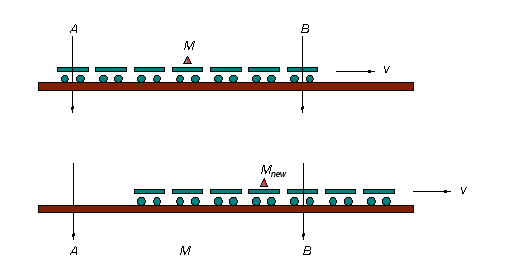
Figure 1. Einstein’s example of two simultaneous lightning strokes down to points A and B.

Another frame of reference (set of rulers) can be constructed and placed on a rotating merry-go-round. The position of any object (say for example an insect sitting still on the merry-go-round) can be measured by both of these frames of reference. In one of them (the one on the merry-go-round) the insect’s velocity is zero. The other frame of reference would describe the insect as moving in a circle. When one frame of reference is moving with respect to another frame of reference, different measurements of motion will be recorded by the same event.

An example of this is the so-called Coriolis effect. Suppose we have a stationary circular merry-go-round on which two people stand facing each other at the ends of a diameter of the disk. One throws a ball directly toward the other person who catches it. Both our frames of reference (one attached to the ground and one sitting on the merry-go-round) would report that the ball had traveled in a straight line when viewed from above.

Now rotate the merry-go-round in a counter-clockwise direction (looking down at it from above) at a constant angular velocity. We can see the path of the ball by placing a downward looking TV camera above the merry-go-round. But if the camera is fixed to the stationary Earth, we will see that although the ball initially moves directly toward the other person, he will be rotated away from his initial location and not be there to catch it when the ball arrives. Because the ball still travels in a straight line.

If we mount another downward looking camera – this one fixed to the rotating merry-go-round – the two people will appear to be stationary and the ball will appear to curve off to the right. This effect is demonstrated on several Youtube presentations.⁵ It is important to realize that the perception the observer gets about what is occurring depends on which frame of reference he is in.

Ratcliffe describes an experiment proposed by Einstein that involves an observer riding on a railroad train. Two simultaneous lightning strokes occur – one from the sky down to point A on the ground and the other down to point B. At that instant the train happens to be located such that its front end is passing over point A and its back end over point B. The situation is shown in the top diagram in figure 1 above.

The train is moving with constant velocity v toward the right. Assuming light propagates with a finite velocity, the observer at point M is unaware of the flashes until a time, T, has passed. But the train has moved toward the right during that time interval. The lower diagram shows the position of the train after time, T, has passed. The observer, now at position M_new, sees the flash from stroke B. But because the light from A has farther to travel, he still is unaware of it.

Therefore, the observer perceives that stroke B has occurred prior to stroke A. The reason for this is, of course, that the observer’s frame of reference is moving relative to the stationary “inertial” frame – the Earth. Einstein then goes on to conclude that, in the frame of the observer, which is moving toward the right, the two events were really not simultaneous.

Can you see the error? If he had said that the observer’s perception of what happened was that stroke B occurred first, he would have been correct. But his interpretation was that, within the moving frame of the observer the two events were in reality not simultaneous.

Einstein confused the observer’s perception of reality with reality itself.

Another even more confusing and erroneous interpretation of what actually happened in this experiment is that time, as measured by a stopwatch held by the observer, slowed down. This is because the interval between stroke B and its observation at M_new is too short. The moving stopwatch measured too few nanoseconds – so Einstein said, “Clocks in a moving frame of reference slow down.” Of course, this is nonsense.

Ratcliff easily falsifies the hypothesis that a moving clock slows down via the following example. Consider two clocks, A and B, moving toward each other along a straight line joining them. Relativists consider that a clock that is moving within any frame of reference with respect to one that is fixed to that frame, runs slow. Referred to A, B goes slow. Referred to B, A goes slow. But they cannot each go slower than the other one. So the idea is mutually contradictory.

To quote Ratcliffe, “The mistake [Einstein] makes, one he commits consistently throughout development of Special Relativity Theory, is that he confuses his frames of reference and does not adjust for varying travel times of constant-velocity signals covering different distances.”

I would add that, more importantly, Einstein mistakenly glosses over the distinction between an observer’s perception of reality and reality itself. Reality exists. Reality will continue to exist even after you and I both die and are unable to perceive it.

If Einstein had observed the Coriolis experiment that involved throwing a ball across a rotating merry-go-round, he would have falsely concluded that the ball really did curve in the “reality” of the rotating frame of reference. That is what the observer perceived. But that’s not what happened. “Seeing is believing” is sometimes “seeing is misleading”. An observer’s perceptions must not be improperly upheld as being of equal validity with reality. Perceptions are often inaccurate.

“My reality is just as valid as your reality” is not universally true.

Ratcliffe’s The Virtue of Heresy provides a sound, accessible critique of fundamental logical errors in SR and GR that have been unnoticed in the past, even by people with outstanding physics and mathematical backgrounds. He attacks the basic foundations of Einstinian theory with clarity, counter-examples, and sharp dissection of some of the imprecise “gedanken-experimental results” and “observations” that are thrown up in support of these notions.

This book is a powerful resource. When taken together with Steve Crothers’ devastating analyses of errors in the tensor analyses that have here-to-fore been effectively raised as an impenetrable barrier to any criticism of SR and GR normally intelligent people need no longer feel intimidated.

We must remember that the erroneous Ptolemaic Earth-centered universe model lasted for at least a thousand years. But that was before enquiring minds had access to books and the Internet. Possibly we will now not have to wait that long for the false SR and GR theories to be put to rest.

Contributed by D. E. Scott