From Ptolemy to Dark Matter - Part 2
Feb 06, 2009

Beginning with the assumption that gravity is the dominant force in galactic dynamics generates complicated models to compensate for the missing piece of the puzzle. Similarly, assuming that the Earth is the center of all things creates models that are required to compensate for that initial assumption. Indeed, it is interesting to consider some of the properties of the Ptolemaic system with that of the new dark matter paradigm.

In the Ptolemaic system, the dynamics of the solar system were driven by spheres that are invisible. In the dark matter system, galaxy dynamics are driven by multiple invisible haloes (envisioned as oblate spheroids) surrounding the galaxy. The dark matter haloes cannot be directly observed. It is their indirect action on the dynamics of the galaxy that is observed, much like the Ptolemaic spheres were inferred by the motion of the heavenly bodies. 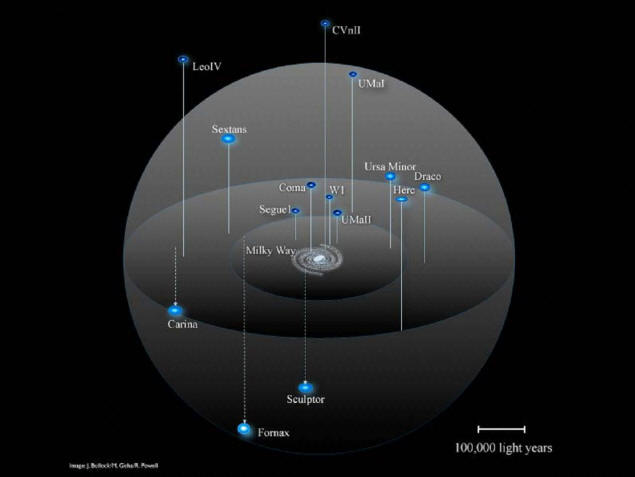The number of dark matter halos and subhaloes for a Milky Way-type galaxy can be quite high, as some recent computer modeling shows.

The “Via Lactea" (Latin for Milky Way) project provides “high resolution Milky Way dark matter haloes simulated on NASA's Columbia and ORNL's Jaguar supercomputers.” Obviously, if cold dark matter in an actual galaxy cannot be observed, the best thing to do is to create an artificial universe to do experiments instead. The most recent Via Lactea simulations show that there are about 10,000 dark matter subhaloes in the Milky Way galaxy. The computational power available to Diemand et al. has also allowed them to “resolve” fine structure in the dark matter haloes. Their images of the concentric shells of dark matter around the simulation galaxy Via Lactea are eerily similar to Ptolemaic models for the solar system.

One wonders what Ptolemaic astronomers might have “discovered” if given access to NASA’s funding and supercomputers. How well would they have refined their equant values to derive more accurate predictions? How many spheres would the planets have acquired? In their model there were about five spheres per planet. With NASA’s Columbia supercomputers, they would have been able to model with greater precision and perhaps they would have “discovered” 10,000 celestial spheres per planet instead of just five. Perhaps they could have resolved finer granular structures in the sub-spheres?

Computer modeling work aside, the influence of the Gravity Assumption is insidious in the way it colors the reporting of new findings of real galaxies. In a recent report, researchers infer from the measure of galactic masses that there is some “minimal mass” for small satellite galaxies around the Milky Way galaxy. The original paper describes velocity measurements that were extended out to about 0.3 kilo-parsecs (kpc) from the center of each galaxy. The paper reports that “...all 18 dwarf galaxies are consistent with having a dynamical mass of 10^7 solar masses within 0.3 kpc of their centre.” Another way of stating this is that all 18 dwarf galaxies are consistent with having similar dynamical measurements of velocity within 0.3 kpc of their center.

The equation to derive mass uses radius (about 0.3 kpc for each galaxy), the gravitational constant (G), velocity and mass. So, if mass was found to be relatively constant across these 18 galaxies, it means that the velocity measurements were also relatively constant across these 18 galaxies. It is relatively easy to derive the rough velocity dispersion associated with a galaxy of 10^7 solar masses and radius of 300 kpc. In fact, it works out to an order of magnitude of 10 km/s.

This agrees well with a paper by Walker et al. (2007) where they focused on the velocity dispersion among seven of these same Milky Way satellite galaxies. They found that the velocity dispersions of these seven galaxies were all in the range of 10 km/s. Very importantly, in all these small galaxies the velocity dispersion was very flat from about 100 parsecs to beyond the visible matter in the galaxy (> ~1000 parsecs).

So, the question is really why do all these satellite galaxies have similar rotational velocities? It is not about mass. Mass is based on the assumption that gravity dominates the dynamics. The real observational quantity here is the relatively constant value for velocity dispersion amongst these satellite galaxies. Using the ideas of Alfvén above, one might assume that these satellite galaxies are formed in the z-pinches of Birkeland currents experiencing similar current density, thus generating similar rotational velocities.

For example, imagine in the figure at the top of this article that the Milky Way is formed in the z-pinch of two large intertwining Birkeland filaments. Surrounding these two larger twisting filaments are smaller filaments self-organized into like-sized filaments twisting in pairs around the larger core filaments. This is a way that Birkeland currents can organize themselves which explains the eerily perfect hexagonal shape of Saturn’s north pole and many hexagonal craters.

These like-sized peripheral filaments will have like-sized current densities. It would follow that the peripheral filaments would twist and form z-pinches creating smaller “satellite” galaxies. In essence, these peripheral filaments are “mopping up” the remaining dust and matter left over from the z-pinch in the core filaments that formed the Milky Way.

The amount of luminous mass in the galaxy has no effect on the inherent rotational dynamics of the driving Birkeland current. The electromagnetic forces of the plasma filaments dwarf the gravitational potential of the matter captured in the z-pinch. The masses of these satellite galaxies are quite different from each other because there is no dark matter making up for gravity’s inability to drive these rotational velocities. Their rotational velocities are quite similar because they are driven by similar Birkeland currents that exhibit similar rotational energies.

One is likely to assume that the sun revolves around the Earth because the Earth is solid and does not appear to move. In the past, our everyday experience led us to make that fundamental assumption. It took us several hundred years to overcome the strength of that perception. Similarly, we have no everyday sense of the scale of electromagnetic plasma forces at work in galaxies or our own solar system. Gravity dominates our view of the cosmos because gravity dominates as a force in our everyday existence. It may take us a long time to let go of gravity as an important organizing force at the cosmic scale.

Contributed by Thomas Wilson