|
|
Chapter 4: Electromagnetism
4.1 The Electromagnetic Field Equation
|
Science attempts to explain physical systems in terms of mathematical models which describe and predict the behavior of the system. For example, Kepler explained the movement of the planets with his three laws. In the same way, plasma behavior is governed by the electromagnetic field equations, which describe the motions of charged particles and their interaction with electric and magnetic fields. There are two components of the electromagnetic field equations: Maxwell's Equations and the Lorentz Force Law. The two components act in tandem as a feedback loop:
Maxwell's Equations determine the electric and magnetic fields based on the position and motion of charged particles. They also determine the interaction of the electric and magnetic fields if either is changing.
The Lorentz Force Law determines the electric and magnetic forces on a charged particle moving within the fields. This force will cause each particle to move (accelerate) in accordance with Newton's Laws. The change in the position and motion of the charged particles causes changes in the electric and magnetic fields.
This feedback loop can rapidly cause highly complex behavior, which is extremely difficult to model mathematically. Simplifications are often introduced. However, simplifying assumptions often lead to the omission of precisely those sorts of behavior which distinguish plasma behavior from that of a gas or other fluid.
|
|
|
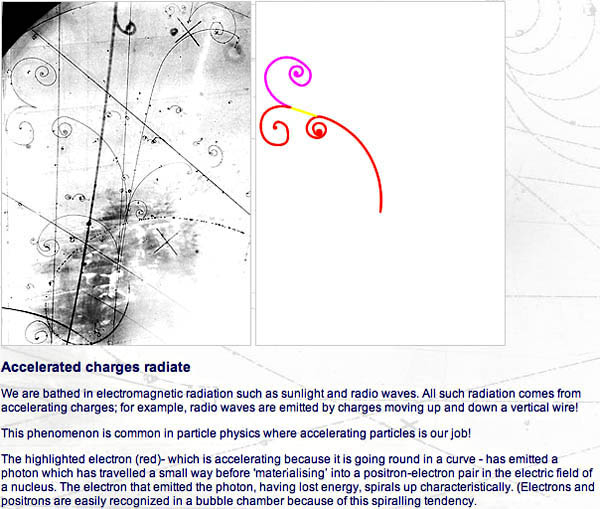
Bubble chambers with magnetic fields create visible tracks of charged
particles, allowing evaluation of particle interactions and collision
by-products when installed in line with a particle accelerator.
Image credit: Bubble chamber tutorial provided by
CERN
at this web site.
|
|
|
A full description of the electromagnetic field equations can be found in Appendix II. What follows is a summary of the key points
4.2 Maxwell's Equations
The implications of Maxwell's Equations and the underlying research are:
- A static electric field can exist in the absence of a magnetic field; e.g., a capacitor with a static charge Q has an electric field without a magnetic field.
- A constant magnetic field can exist without an electric field; e.g., a conductor with a constant current I has a magnetic field without an electric field.
- Where electric fields are time-variable, a nonzero magnetic field must exist.
- Where magnetic fields are time-variable, a nonzero electric field must exist.
- Magnetic fields can only be generated in two ways other than by permanent magnets: by an electric current, or by a changing electric field.
- Magnetic monopoles cannot exist; all lines of magnetic flux are closed loops.
4.3 The Lorentz Force Law
The Lorentz Force Law expresses the total force on a charged particle exposed to both electric and magnetic fields. The resultant force dictates the motion of the charged particle by Newtonian mechanics. As the Lorentz equation is fundamental to all plasma behavior, it is worth spending a little time understanding what it means. The equation is:
|
|
|
|
F = Q(E + U x B)
|
|
|
(Vectors are given in bold text and explained below)
where F is the Lorentz force on the particle; Q is the charge on the particle; E is the electric field intensity; U is the velocity of the particle; B is the magnetic flux density, and x is the vector cross product symbol, not merely a multiplication sign. Read it as "U cross B".
In order to understand what the equation actually means, we need to know a little about vectors.
A vector is a quantity which has both magnitude and direction. Examples include velocity and force. It's like an arrow -it has a length and it points in a direction. By contrast, a scalar quantity only has magnitude. Examples include speed and temperature. Vector algebra is the mathematics which deals with vectors. For those wanting to know, further details of vector algebra are given in Appendix III. The essentials for understanding the Lorentz equation will be explained here.
First, multiplying a vector by a scalar quantity is like putting a number of similar arrows together end to end. The vector is the first arrow; the scalar quantity is the number of similar arrows. The result is a bigger arrow in the same direction as the original vector.
Multiplying two vectors together is more complicated. Think of a very large screw in a board where the slot in the head represents the first vector and the second vector is drawn on the board. As the screw is twisted clockwise until the slot aligns with the second vector, the screw will move into the board at right angles to both the slot and the second vector. The amount of movement depends on the dimensions of the screw and the amount it is turned. The vector cross product is a bit like this.
Multiplying two vectors together using the cross product results in another vector at right angles to both the previous vectors. The direction of the new vector is given by the direction of movement of our imaginary screw. The size of the new vector depends both on the angle turned and on the size of the original vectors.
As in the case of our screw, if the vectors are aligned (parallel) in the first place, then no movement of the screw takes place. The cross product of aligned vectors is zero.
More formally, in Cartesian coordinates, if a vector in the x direction is crossed with a vector in the y direction, then the result is a vector in the z direction. The magnitude of the resultant vector is the triple product of the lengths of the two original vectors and the sine of the smaller angle between them. If they are parallel, the angle between them is zero. Since sin(0°) is zero, in that case there is no resultant force in the z direction.
The effect is very similar to the gyroscopic effect in rotating solids: a force in one direction results in motion in a direction at right angles. This is known as precession.
Going back to the Lorentz Force Law, we see that the total force is made up of two parts. The first part is QE, which is the product of the scalar value of the charge on the particle and the electric field strength vector. The magnitude of the force due to the electric field is the product of the charge on the particle and the strength of the electric field.
Note that the force due to the electric field is constant and in the direction of E, so it will cause constant acceleration of the particle in the direction of E according to Newton's Laws of Motion, one way for a positive charge, and the opposite for a negative charge.
The second part of the equation, Q(U x B) is more interesting. Here we have two vectors multiplied together using the cross product and then multiplied by the charge on the particle. Assuming that the particle was not moving in alignment with the field in the first place, when the force would be zero, then the result will be a force which is at right angles to the direction of motion of the particle and the magnetic field.
This explanation
of The Right Hand Rule will explain the "steering" force that a magnetic field in some direction exerts on a charged particle entering the field.
A force at right angles to the motion is a centripetal force. The magnetic field will therefore cause the charged particle to move in a circle in a plane perpendicular to the direction of the magnetic field. As the particle is moving round the circle its velocity at any point will still be at right angles to the magnetic field, and so it will still experience a centripetal force which keeps it moving in the circle.
A simple case is to consider what happens when a moving charged particle enters a (fixed) magnetic field. We will ignore any effects that the particle might have upon the magnetic field. If it enters the field paralle to the direction of the field it experiences no force and nothing about its velocity or direction changes. If it enters the field at a right angle to the direction of the field, its path will simply curve into a circle which closes upon itself.
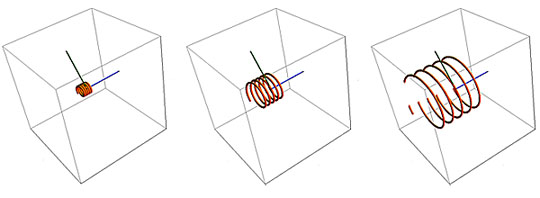
Without an electric field, the Lorentz law reads (centripetal force) F = Q(U x B). The force applied to the charged particle is directly proportional to Q, the particle's charge, to U, the velocity vector, and to B, the magnetic field vector. The meaning of U x B is U times B times the sine of the smaller angle between the two vectors, which means that UB is multiplied by the sine of an angle, so its effect ranges from zero to 1. In the comparative illustration below, the particle's charge and the magnetic field are held constant and the velocity of the particle as it enters the field increases from left to right. The faster the particle is moving, the larger the radius of the resultant circular motion, because the radius r is a measure of the particle's linear momentum mU where m is the particle mass: r = mU/|Q|B . The same result would apply if the charge were to increase while the other two variables were held constant.
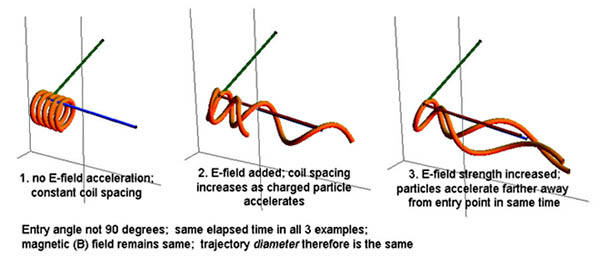
If it enters the magnetic field with a component of motion in the direction of the field, i.e., at an angle between zero and 90 degrees to the field direction, it will "drift" in the direction parallel with the field, while the field forces the particle into a circular motion. This "drifting" circular path traces out a helix or spiral. The "guiding center" of the circle follows a field line of the magnetic field. The radius is known as the Larmor radius. In the three illustrations below, the angle of entry by the particle and the strength of the magnetic field, B, remain the same, with a small drift motion toward the left. The initial entry velocity increases step-wise from left to right.
In the series of images below, the green entry vector touching the magnetic and electric field lines shows which way a positively charged particle (by convention) is moving as it "enters" the field(s). The particle may be going in either direction along this vector line at entry, so there are two trajectories coming out of the tip of the green vector, as you will see. If the particle were charged negatively, it would accelerate in the opposite direction, and if it were heavier or moving faster, it would have a larger diameter circle than depicted. Similarly, if the magnetic or electric fields were changed, holding other factors constant, that would similarly change the particle's behavior. The narrow orange "tubes" represent the particle's trajectory resulting from the entry conditions.
|
|
|
As a charged particle enters a magnetic field, its path is bent into a
circle whose radius r is proportional to its linear momentum, m times U:
r = (mU) ÷ (|Q|B), where U is the magnitude of its velocity, m = mass.
The particle's velocity does not change, so its kinetic energy is unchanged,
and the field does no work on the particle. This is analogous to gravity's
exerting a continuous centripetal force on an orbiting satellite in space.
Magnetic field direction is shown by blue axial line; entry angle by green radial line.
|
|
|
|
|
|
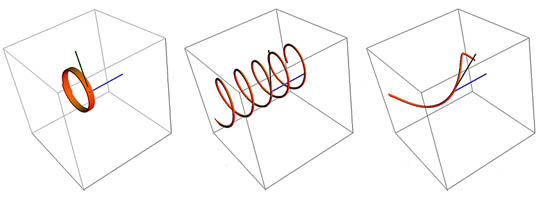
Changing entry direction of the charged particle from normal
to the magnetic field to parallel with the magnetic field will
stretch the spiral path out and decrease the radius toward zero.
Note the changing entry vector, left to right, and the helical stetching
Images above created with Mathematica Demonstrations
|
|
|
The total force will be the vector resultant of the electric and magnetic forces and depends on the angle between the two fields.
If the electric and magnetic fields are parallel (as in the field-aligned current situation we will consider later), then a charged particle approaching radially towards the axial direction of the fields will be constrained to move in a helical path aligned with the direction of the fields. That is to say, the particle will spiral around the axial direction of the magnetic field as a result of the Lorentz force, accelerating in the direction of the electric field. This makes succeeding revolutions farther and farther apart as the particle's velocity in the E-field direction increases over time.
|
|
|
In a field-aligned situation (E and B fields parallel), a particle
trajectory has the centripetal magnetic force applied at the same
time that the E-field vector (red) forces it to accelerate axially so that
so that over time the particle is moving nearly parallel to the fields.
|
|
|
If the particle enters the combined, aligned field axially, it experiences no magnetic field so force to revolve around a guiding center is not exerted. The electric field, however, will accelerate the particle along the field lines. Depending on its charge, if the particle enters in the direction of the accelerating force, its velocity increases. If it enters counter to this force, it decelerates and may stop and accelerate back in the opposite direction.
If the fields are not aligned, various trajectory combinations can occur depending on the particulars of the charge, field strengths, entry direction and angular misalignment of the magnetic and electric fields.
|
|
|

With a constant electric field present, its general tendency
will be to accelerate particles ever more closely aligned with
its field lines, and to increasing velocities.
Images above created with Mathematica Demonstrations
|
|
|
Although these trajectories may look complex, they involve only a single charged particle at a time, with constant electric and magnetic fields, with the same entry velocity. In practice many charged particles may occupy a volume of space at once, and their electric and magnetic interactions can affect the field values in which they move.
There may also be neutral particles present, as well as dust and grains and large bodies, all of which may exert other forces on the plasma interactions, too.
We note in passing that secondary effects of electrons spiraling around magnetic field lines in space are often detected in the form of synchrotron radiation. From consideration of the Lorentz Force Law, we know that there must therefore be an electric field aligned with the magnetic field and that the axial movement of the spiraling electrons constitutes a field-aligned current.
4.4 Other Effects of the Field Equation
It is worth remembering some basic results arising from the application of the electromagnetic field equations.
- Electric fields cause a force on all charged particles.
- The electric force will be in opposite directions for oppositely charged particles; therefore, an electric field will produce opposite velocities of ions and electrons and so tend to separate them.
- Magnetic fields only act on moving charged particles. Because the force depends on the cross-product of the velocity and field vectors, the effect will be different in different directions. This results in a direction-dependent electrical resistance.
- The magnetic force is charge-dependent; ions and electrons will therefore circle in opposite directions with different radii and periods.
- Bulk plasma moving across the direction of a magnetic field will cause a local electric field to develop which itself will cause new forces on the charged particles.
- Changes in the distribution of charged particles cause a change in the electric field between them; a changing electric field generates a change in the magnetic field.
- The Maxwell Equations and the Lorentz Force Law act together as a feedback loop modifying the motions of the charged particles and the fields in complex ways.
4.5 Replacing Currents with Magnetic Fields
The question arises as to whether electric currents can be replaced by magnetic fields using Maxwell's Equations, which would make the solutions much easier.
The answer is, technically, yes they can in certain simple situations, and this is often done in magneto-hydrodynamic theories because it is more convenient for studying certain plasma phenomena. However, there are many aspects of plasma behavior where it is necessary to consider the movement of the charged particles because simply considering the field behavior cannot model the observed complexity of plasma behavior.
The situation is analogous to the wave-particle duality in particle physics: there are some situations where it is necessary to use the particle description.
Examples of plasma behavior requiring use of the particle or current description include cellularization and filamentation, energy transport, and instabilities. Consideration of electric currents and circuits also necessitates the use of a particle-based description.
Simply considering only the field effects in these situations will miss the true complexity of plasma behavior. We shall look at some of these more complex behaviors next.
|
|
end of Chapter 4
|
next: Chapter 5: Plasma Sheaths, Cells and Current-Free Double Layers
previous: Chapter 3: Plasma
|
|
|
Permalink to this page
return to Preface & Table of Contents
|
|
|
|
|
|
|